Portfolio optimisation approach combining quantum meta-heuristics and mathematical programming.
Introduction
Portfolio optimisation is a process used in finance to select the best portfolio (collection of assets) from a suite of potential portfolios that meet certain criteria. The objective – return optimisation, risk mitigation or both, among others – can vary, based on the goal of an investor. The Markowitz mean-variance optimisation model stands out as the most widely accepted formula to generate the best possible asset mix that fits an investor’s requirements.
Since Markowitz model relies on certain assumptions, it does not paint a realistic picture of the market. Thus, it is time to introduce advanced computational methodologies, particularly quantum computing, to relax some of these assumptions of the vanilla Markowitz model and reformulate the model. This study aims to cap one such assumption of the vanilla Markowitz model which says that assets are infinitely divisible. However, as we attempt to make the model more realistic, the generated results from the quantum computing approach might be suboptimal compared to the original model. This highlights the need for further research into possible enhancements of the reformulated model.
Quantum computing
IBM defines quantum computing as the use of specialised computer hardware and algorithms to solve problems that are unsolvable or hard to solve using classical computers (IBM, 2024).
Quantum computing solves some problems beyond the realm of classical computing. For example, Quantum annealers are a specific type of quantum computer designed to solve optimisation problems, particularly those that are NP-hard or NP-complete, using the principles of adiabatic quantum computing. The first commercially available quantum computer – the D-Wave One (built in 2011) – was based on quantum annealing.
Reformulation of markowitz optimisation problem into integer program
To address unrealistic assumptions in the original Markowitz model, this paper suggests some changes to the decision variables and introduces additional constraints to the model, enhancing its applicability in real-world financial contexts.
Implementation
After finalising the equation, an algorithm was developed using Python to generate the intended results. Then, using real-time quantum cloud service provided by D-wave, Leap, the algorithm was fitted to the daily profit of 113 stocks obtained from Yahoo Finance and the following values were set for constraints:
- Risk/standard deviation (R) – 0.01
- Sum of shares (S) – 1,000.
The objective was to optimise the portfolios’ expected return subject to the above constraints. Furthermore, the data used for optimisation was limited to 2000-2016. Stock values from 2017-2019 was used for testing, and the 2020-2023 data was used as out-of-sample testing data.
Results
After running the reformulated algorithm, we were left with a portfolio of 78 stocks, which generated a 0.07% return under a risk of 1%. Furthermore, the algorithm successfully satisfied all the constraints set earlier.
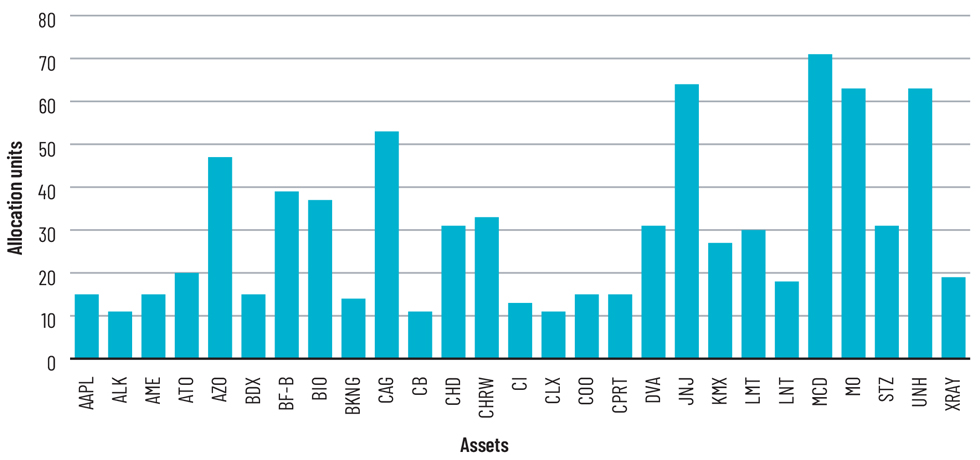
(unlike the vanilla Markowitz model, the output was the number of units to be purchased from each stock)
On the other hand, the classical algorithm generated a portfolio of 19 stocks with a return of 0.09% under a risk of 1%.
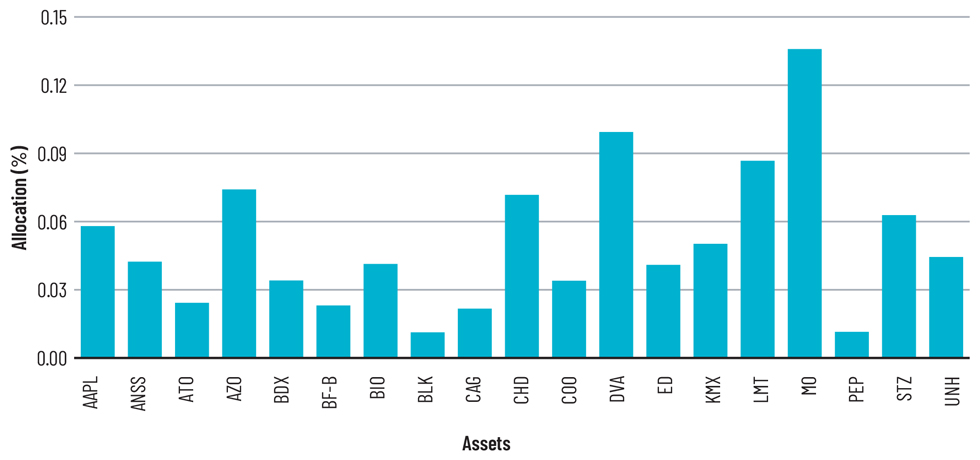
Of the 113 stocks we had initially, both the models converged towards a similar set of stocks for inclusion in the portfolio. This highlights that the two models go hand in hand, underscoring a strong correlation between the decision-making processes.
Conclusion
It is possible to find a global optimum for the vanilla optimization problem by using classical computers, as it is a convex continuous problem. However, one of the key issues we try to address through the study is the assumption that assets are infinitely divisible; hence a reformulated model is proposed.
Although the reformulated model is more realistic, it introduces an integer programming problem, which cannot be solved efficiently through classical computers. This brought about the need for the quantum annealer which brings in a QUBO formulation by D-Wave, and, hence, it is possible that the returns obtained is still a sub-optimal solution. Thus, we get a lower return for the quantum solution in comparison to the vanilla model.
In conclusion, this study serves as an invitation to the research community to explore and use quantum computing for portfolio optimisation. Diving further, one can use the quantum advantages not only to relax some other unrealistic assumptions of the Markowitz model, but also to tailor the optimisation problem to suit business requirements.
While quantum computing is one of Acuity’s niche cutting-edge technology offerings, you can refer to our financial services technology consulting solutions for details on all of our data and technology solutions for the financial services industry.
Thank you for sharing your details
Share this on
